توزیع نرمال استاندارد یکی از پرکاربردترین توزیعها برای محاسبه احتمالات و مفاهیم مرتبط با اکثر پدیدههای طبیعی است. چرا که اولا بسیاری از پدیدههای طبیعی دارای این توزیع هستند و در ثانی قابل اثبات است که شکل حدی بسیاری از توزیعهای دیگر، نرمال است.
با توجه به شکل این توزیع و تابع چگالی آن مسلما انتگرال گرفتن از آن و محاسبه احتمالات مربوط به آن کاری بسیار وقت گیر و طاقت فرسا خواهد بود. از این بابت دانشمندان با تبدیل نمودن توزیعهای نرمال به یک توزیع استاندارد که میانگین آن صفر و انحراف معیار آن یک است مسیر محاسبه احتمالات را بسیار کوتاه نمودهاند. از این بابت با یک تبدیل ساده هر توزیع نرمال را میتوان به سادگی به توزیع نرمال استاندارد تبدیل نمود و احتمالات محاسبه شده برای هربخشی از آن را از جدول توزیع نرمال استاندارد به دست آورد.
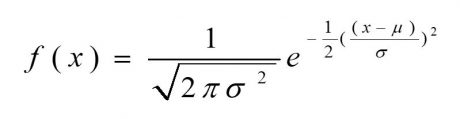
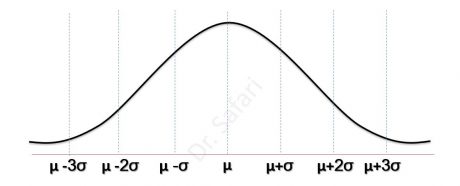
هنگام استفاده از جدول نرمال همواره باید به توضیحات بالای جدول دقت کنیم و ببینیم جدول برای چه مقادیری ارائه شده است.
جدولی که در زیر مشاهده می کنید سطح زیر منحنی را از نقطه ی صفر تا z ارائه می کند.
برای مشاهده مقادیر سطح زیر منحنی توزیع Z نرمال استاندارد، از جدول زیر استفاده نمایید. در انتهای صفحه نیز مقادیر نقاط ∝ درصد توزیع Z درج شده است.
جدول توزیع نرمال استاندارد یا جدول Z، احتمالات مربوط به مقادیر مختلف متغیر تصادفی پیوسته نرمال را ارائه میکند.
| 0.09 | 0.08 | 0.07 | 0.06 | 0.05 | 0.04 | 0.03 | 0.02 | 0.01 | 0.00 | Z0 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0358 | 0.0318 | 0.0279 | 0.0239 | 0.0199 | 0.0159 | 0.0119 | 0.0079 | 0.0039 | 0 | 0.0 |
| 0.0753 | 0.0714 | 0.0674 | 0.0635 | 0.0596 | 0.0556 | 0.0517 | 0.0477 | 0.0437 | 0.0398 | 0.1 |
| 0.1140 | 0.1102 | 0.1064 | 0.1025 | 0.0987 | 0.0948 | 0.0909 | 0.0870 | 0.0831 | 0.0792 | 0.2 |
| 0.1517 | 0.1480 | 0.1443 | 0.1405 | 0.1368 | 0.1330 | 0.1293 | 0.1255 | 0.1217 | 0.1179 | 0.3 |
| 0.1879 | 0.1843 | 0.1808 | 0.1772 | 0.1736 | 0.1700 | 0.1664 | 0.1627 | 0.1590 | 0.1554 | 0.4 |
| 0.2224 | 0.2190 | 0.2156 | 0.2122 | 0.2088 | 0.2054 | 0.2019 | 0.1984 | 0.1949 | 0.1914 | 0.5 |
| 0.2549 | 0.2517 | 0.2485 | 0.2453 | 0.2421 | 0.2389 | 0.2356 | 0.2323 | 0.2290 | 0.2257 | 0.6 |
| 0.2852 | 0.2823 | 0.2793 | 0.2763 | 0.2733 | 0.2703 | 0.2673 | 0.2642 | 0.2611 | 0.2580 | 0.7 |
| 0.3132 | 0.3105 | 0.3078 | 0.3051 | 0.3023 | 0.2995 | 0.2967 | 0.2938 | 0.2910 | 0.2881 | 0.8 |
| 0.3389 | 0.3364 | 0.3339 | 0.3314 | 0.3289 | 0.3263 | 0.3238 | 0.3212 | 0.3185 | 0.3159 | 0.9 |
| 0.3621 | 0.3599 | 0.3576 | 0.3554 | 0.3531 | 0.3508 | 0.3484 | 0.3461 | 0.3437 | 0.3413 | 1.0 |
| 0.3829 | 0.3809 | 0.3789 | 0.3769 | 0.3749 | 0.3728 | 0.3707 | 0.3686 | 0.3665 | 0.3643 | 1.1 |
| 0.4014 | 0.3997 | 0.3979 | 0.3961 | 0.3943 | 0.3925 | 0.3906 | 0.3887 | 0.3868 | 0.3849 | 1.2 |
| 0.4177 | 0.4162 | 0.4146 | 0.4130 | 0.4114 | 0.4098 | 0.4082 | 0.4065 | 0.4049 | 0.4031 | 1.3 |
| 0.4318 | 0.4305 | 0.4292 | 0.4278 | 0.4264 | 0.4250 | 0.4236 | 0.4221 | 0.4207 | 0.4192 | 1.4 |
| 0.4440 | 0.4429 | 0.4417 | 0.4406 | 0.4394 | 0.4382 | 0.4369 | 0.4357 | 0.4344 | 0.4331 | 1.5 |
| 0.4544 | 0.4535 | 0.4525 | 0.4515 | 0.4505 | 0.4494 | 0.4484 | 0.4473 | 0.4463 | 0.4452 | 1.6 |
| 0.4632 | 0.4624 | 0.4616 | 0.4607 | 0.4599 | 0.4590 | 0.4581 | 0.4572 | 0.4563 | 0.4554 | 1.7 |
| 0.4706 | 0.4699 | 0.4692 | 0.4685 | 0.4678 | 0.4671 | 0.4663 | 0.4656 | 0.4648 | 0.4640 | 1.8 |
| 0.4767 | 0.4761 | 0.4755 | 0.4750 | 0.4744 | 0.4738 | 0.4731 | 0.4725 | 0.4719 | 0.4712 | 1.9 |
| 0.4816 | 0.4812 | 0.4807 | 0.4803 | 0.4798 | 0.4793 | 0.4788 | 0.4783 | 0.4777 | 0.4772 | 2.0 |
| 0.4857 | 0.4853 | 0.4849 | 0.4846 | 0.4842 | 0.4838 | 0.4834 | 0.4829 | 0.4825 | 0.4821 | 2.1 |
| 0.4889 | 0.4886 | 0.4883 | 0.4880 | 0.4877 | 0.4874 | 0.4871 | 0.4867 | 0.4864 | 0.4860 | 2.2 |
| 0.4915 | 0.4913 | 0.4911 | 0.4908 | 0.4906 | 0.4903 | 0.4900 | 0.4898 | 0.4895 | 0.4892 | 2.3 |
| 0.4936 | 0.4934 | 0.4932 | 0.4930 | 0.4928 | 0.4926 | 0.4924 | 0.4922 | 0.4920 | 0.4918 | 2.4 |
| 0.4952 | 0.4950 | 0.4949 | 0.4947 | 0.4946 | 0.4944 | 0.4942 | 0.4941 | 0.4939 | 0.4937 | 2.5 |
| 0.4964 | 0.4963 | 0.4962 | 0.4960 | 0.4959 | 0.4958 | 0.4957 | 0.4956 | 0.4954 | 0.4953 | 2.6 |
| 0.4973 | 0.4972 | 0.4971 | 0.4971 | 0.4970 | 0.4969 | 0.4968 | 0.4967 | 0.4966 | 0.4965 | 2.7 |
| 0.4980 | 0.4980 | 0.4979 | 0.4978 | 0.4978 | 0.4977 | 0.4976 | 0.4975 | 0.4975 | 0.4974 | 2.8 |
| 0.4986 | 0.4985 | 0.4985 | 0.4984 | 0.4984 | 0.4983 | 0.4983 | 0.4982 | 0.4981 | 0.4981 | 2.9 |
| 0.4989 | 0.4989 | 0.4989 | 0.4988 | 0.4988 | 0.4988 | 0.4987 | 0.4987 | 0.4986 | 0.4986 | 3.0 |
همچنین بر اساس جدول زیر نیز میتوانید مقادیر نقاط ∝ درصد توزیع Z را به دست آورد.
اگر ∝ عددی بین صفر و یک باشد و سطح زیر منحنی نرمال استاندارد از نقطه ∝Z تا ∞ + برابر ∝ باشد، آنگاه ∝Z را نقطه ∝ درصد توزیع نرمال میگوئیم.
P(Z > Z∝) = ∝
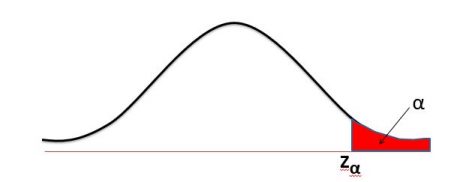

برای آشنایی با نحوه استفاده از این جدول میتوانید ویدئو آموزشی زیر را که توسط آقای دکتر خلیل صفری آموزش داده شده است را مشاهده نمایید.










۰ پاسخ به "جدول توزیع نرمال استاندارد و نحوه استفاده از آن"